by Amy S. Ludtke, Mark T. Woodworth, and Philip S. Marsh

by Amy S. Ludtke, Mark T. Woodworth, and Philip S. Marsh |
 |
U.S. GEOLOGICAL SURVEY |
An overall evaluation of the inorganic and low-level constituent data for water year 1998 indicated 77 of 78 analytical procedures at the National Water Quality Laboratory met the criteria for precision. Silver (dissolved, inductively coupled plasma-mass spectrometry) was determined to be imprecise. Five of 78 analytical procedures showed bias throughout the range of reference samples: chromium (dissolved, inductively coupled plasma-atomic emission spectrometry), dissolved solids (dissolved, gravimetric), lithium (dissolved, inductively coupled plasma-atomic emission spectrometry), silver (dissolved, inductively coupled plasma-mass spectrometry), and zinc (dissolved, inductively coupled plasma-mass spectrometry).
At the National Water Quality Laboratory during water year 1998, lack of precision was indicated for 2 of 17 nutrient procedures: ammonia as nitrogen (dissolved, colorimetric) and orthophosphate as phosphorus (dissolved, colorimetric). Bias was indicated throughout the reference sample range for ammonia as nitrogen (dissolved, colorimetric, low level) and nitrate plus nitrite as nitrogen (dissolved, colorimetric, low level).
All analytical procedures tested at the Quality of Water Service Unit during water year 1998 met the criteria for precision. One of the 63 analytical procedures indicated a bias throughout the range of reference samples: aluminum (whole-water recoverable, inductively coupled plasma-atomic emission spectrometry, trace).
This report describes the results of a quality-assurance program used to monitor the quality of inorganic, nutrient, and low-level analytical procedures at the NWQL and inorganic and nutrient analytical procedures at the QWSU. Previous reports (Peart and Thomas, 1983a, 1983b, 1984; Peart and Sutphin, 1987; Lucey and Peart, 1988, 1989a, 1989b; Lucey, 1989; Maloney and others, 1992, 1993, 1994; Ludtke and others, 1999) document results from February 1981 through September 1997. Some of the previous reports contain quality-assurance information for organic determinations.
The water year used by the USGS is the 12 months from October 1 through September 30 and is identified by the calendar year in which the water year ends. During water year 1998, 95 analytical procedures were evaluated for the NWQL by the Blind Sample Project (BSP). This represents about 85 percent of the inorganic and nutrient analytical procedures offered by the laboratory for water-matrix determinations. The remaining 15 percent of the water-matrix determinations offered were either infrequently requested, so that it was not feasible to include them in the BSP, or the constituents did not have a readily available, stable source of reference material. In addition, the NWQL offers analytical determinations for sample matrices other than water, such as biological tissues and sediments.
The BSP evaluated 63 analytical procedures for the QWSU during water year 1998. This represents about 75 percent of the total number of water-matrix constituents offered for analysis. The remaining 25 percent were considered to be custom determinations that were infrequently requested. In addition, some of the constituents did not have a readily available, stable source of reference material.
Laboratory users who require analyses for water-matrix constituents not offered through the BSP, or any nonwater-matrix determinations, should consider alternative procedures to measure analytical quality. The analytes included in the 1998 NWQL and QWSU BSP are listed below by constituent categories:
Inorganic constituents (NWQL and QWSU BSP's)- alkalinity, aluminum, arsenic, barium, beryllium, boron, cadmium, calcium, chloride, chromium, cobalt, copper, dissolved solids (residue on evaporation at 180ºC), fluoride, iron, lead, magnesium, manganese, mercury, molybdenum, nickel, potassium, selenium, silica, silver, sodium, strontium, sulfate, vanadium, and zinc. Constituents included only in the NWQL BSP were antimony, lithium, and specific conductance (low level). The reference materials used by the BSP are not stable for the higher specific conductance concentration range.
Nutrient constituents (NWQL and QWSU BSP's)- ammonia as nitrogen, ammonia plus organic nitrogen as nitrogen, nitrate plus nitrite as nitrogen, orthophosphate as phosphorus, and phosphorus.
Reference samples for the BSP are made to appear as much like environmental samples as possible to reduce the possibility that analysts will recognize them as quality-assurance samples. Analytical request forms are completed to ensure that appropriate analyses have been requested for the samples. For the NWQL program, samples are delivered by BSP personnel directly to the sample login unit of the laboratory. Because of the great number of samples delivered to the NWQL and because the login unit is separated from the analytical operations, there is little chance that the origin of these quality-assurance samples will be detected. Because the QWSU operation is much smaller than the NWQL and the analysts have direct contact with the sample login operations, the samples and forms are sent to selected USGS offices that use that laboratory. Throughout the year, these offices send the quality-assurance samples for the BSP to the QWSU with their regular environmental samples.
The BSP samples are subjected to laboratory handling, processing, and analytical procedures identical to processes for the environmental samples. After laboratory analysis, BSP personnel compile and review the analytical results. The resulting data are stored in a National Water Information System (NWIS) data base and the BSP's SAS© data base.
The SRWS's are filtered during preparation; therefore, all constituents in the Blind Reference Samples are in the dissolved phase. Constituents that are designated as whole-water recoverable in this report are from filtered reference samples that have undergone a digestion process (Fishman and Friedman, 1989, p. 87-88) rather than from unfiltered or whole-water samples. Differences that appear in this report between the dissolved (DIS) analyses and the whole-water recoverable (WWR) analyses will be due to the digestion process rather than any difference in the sample phase.
The assessments presented in this report are based on analytical results released from the laboratories that have the same level of quality-control review as the data released to each USGS district office. The results presented in the report, however, provide a conservative estimate of the quality of the data stored in individual NWIS data bases because water-quality specialists and project chiefs are expected to scrutinize analytical results for discrepancies, request reruns for questionable results, and update analytical results in the NWIS data base as appropriate.
Factors that need to be considered for interpretation of results stored in NWIS data bases with relation to the results presented in this report include the following:
where the Fourth-spread is analogous to the interquartile range of the data. In addition, they show that the F-pseudosigma yields an unbiased estimate of standard deviation when the data distribution is Gaussian. However, it is recognized that some of the SRWS Project data sets may not have Gaussian data distributions. For non-Gaussian distributions, the F-pseudosigma is still a good estimate of spread and is not unduly influenced by outliers.
The SRWS Project MPV's are used to estimate the BSP mix concentrations that are based on the proportion of the SRWS's used. Likewise, if deionized water is used in the preparation of a blind sample mix, then a sample concentration of zero is applied to estimate the resultant MPV that is based on the proportion used. The resulting MPV's are used in the BSP to compare with analytical results.
For each SRWS constituent, a regression equation was used to estimate the Fs over a continuous range of concentrations. The equations were derived by using ordinary least-squares and regressing the F-pseudosigma against the MPV. The ordinary least-squares regression equation derived for sodium is displayed in figure 1.
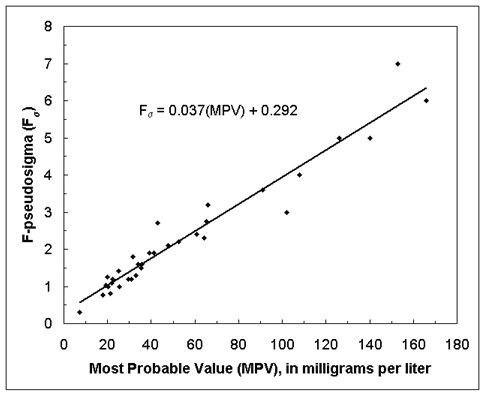
Figure 1. Display of line of relation for ordinary least-squares regression equation derived for sodium.
Helsel and Hirsch (1992) provide a general model for estimation of ordinary least-squares regression:
| where | Fsi | = the ith observation of the response variable, Fs; |
| MPVi | = the ith observation of the explanatory variable, Most Probable Value; | |
| b0 | = the intercept; | |
| b1 | = the slope; | |
| ei | = the random error or residual for the ith observation; and | |
| n | = the number of samples. |
The SRWS Project summary data for semiannual round-robin sample studies conducted during the last 7 years were used to derive regression equations for each analyte. The concentration range of SRWS's used to derive the regression equations, the units of measurement, the derived Fs equation, the number of samples used to derive the equation, and the p-value indicating the level of significance associated with the derived equation are presented in table 1. P-values greater than 0.05 indicate there is less than a 5-percent chance that such a relationship would exist. The null hypothesis for the ordinary least squares regression equation is that no relationship exists between the MPV and the Fs. The authors set a significance level of 0.05. Then the null hypothesis was rejected when the probability, or p-value, was less than or equal to 0.05. Alternatively, when the p-value was less than or equal to 0.05, there is at least 95 percent chance that there is a linear relationship between the MPV and the Fs.
The p-value for fluoride (DIS, IC, LL) is greater than 0.05. All of the MPV's and Fs's used in this regression equation were tightly clustered together. The errors contributed by using this regression equation are very minor, due to the samples low MPV's. For example, the lowest concentration SRWS was 0.04 mg/L and the highest concentration SRWS was 0.139 mg/L. The Fs for each of these samples would be 0.0202 and 0.0207, respectively. In the case of fluoride (DIS, IC, LL), we can conclude that the Fs is close to constant for the narrow range of MPV's analyzed.
The assessment of whether an analytical measurement meets control specifications is based on the number of standard deviations (NSD) that the measured concentration differs from the MPV. In this report, the term standard deviations will be used when comparing individual determinations to the MPV. The NSD is determined by taking the difference between the analytical result and the MPV and dividing by the Fs estimated by the appropriate regression equation using the MPV concentration. Taylor (1987, p. 33-34) provides a general equation that was modified to determine the NSD values for this assessment:
| where | NSD | = number of standard deviations, |
| Xq | = value in question, | |
| MPV | = most probable value, and | |
| Fs | = regression estimate of F-pseudosigma. |
Analytical results that are within two NSD's of the MPV concentration are considered acceptable; however, there have been instances where the assessment criteria, as defined above, resulted in unrealistic tolerances not related to analytical capability but rather to data-reporting criteria set for computer storage of environmental data. This primarily occurred for results near the reporting limits. The numerical precision for computer storage of environmental data is often much less than that used to calculate the MPV's of the SRWS's. For example, the criteria for NWIS data entry for many metals determined by flame-atomic absorption spectrophotometry (F-AAS) is to report values to the nearest 10 µg/L for determinations below 100 µg/L. For the SRWS project round-robin study, however, laboratories typically report data to the nearest 1 µg/L, and the standard deviation for samples with concentrations below 100 µg/L may be only a few micrograms per liter. The regression equations used to estimate Fs are based on SRWS data that are reported with more significant figures, especially at lower concentrations.
The rounding differences between the SRWS summary results and the NWIS computer-storage criteria make the assessments at lower sample concentrations less sensitive. As a means to make the assessments more sensitive at lower concentration ranges, a correction factor has been applied to allow at least one reportable value to be within one standard deviation of the MPV. The correction is accomplished by setting a minimum Fs at three-fourths of the minimum reporting limit. For example, a sample may be assigned an MPV for manganese of 13.7 µg/L; however, the laboratories can only report environmental data for manganese (WWR, F-AAS) to the nearest 10 µg/L in the NWIS data base. For the reference sample in question, a reported value of 10 or 20 would generally be expected. The regression equation for manganese (Fs = 0.047MPV + 0.990) provides an estimate that reported Fs values within ±1.63 µg/L of a sample with an MPV of 13.7 µg/L will be considered within one standard deviation. The laboratories' closest reportable values, 10 and 20 µg/L, would be -2.27 and +3.87 standard deviations, respectively, from the MPV. When a minimum Fs value of 7.5 µg/L is assigned (three-fourths of the reporting limit), then values reported at 10 and 20 µg/L would be -0.49 and +0.84 standard deviations from the MPV, respectively.
BSP mixes that had MPV concentrations less than the laboratory reporting limit (LRL) were removed from the BSP data base. The BSP mixes are not designed to quality assure the laboratories for false positives or for how well the lab reports samples less than the LRL.
For each constituent, the NSD values were plotted against the date that the samples were logged into the laboratory to prepare control charts. The results for each constituent are presented as control charts, as shown in part A of figures 2 through 96 for the NWQL and figures 97 through 159 for the QWSU in the Supplemental Data section of this report.
Control charts for inorganic-constituent reference samples are presented in figures 2 through 79 for the NWQL and figures 97 through 152 for the QWSU. Control charts for nutrient constituents are shown in figures 80 through 96 for the NWQL and figures 153 through 159 for the QWSU. The data on control charts have been separated into quartiles on the basis of environmental sample concentrations. All environmental data released during water year 1998 by the NWQL and QWSU were obtained and used to determine the quartiles. The quartiles and their associated concentration ranges are identified in the figure explanation. The MPV's of the reference materials were examined to determine which quartile group they represented. A different symbol was used to represent data points in each of the quartile ranges. For reference samples with MPV's in quartile 1 (up through 25 percent), the (l) symbol has been used; reference samples in quartile 2 (25.1 through 50 percent) are represented by the (l) symbol; quartile 3 (50.1 through 75 percent) by the (l) symbol; and quartile 4 (75.1 through 100 percent) by the (l) symbol.
Points on the control charts that are greater than 6 standard deviations or less than -6 standard deviations have been rounded to 6 and -6, respectively, and are plotted at the top or bottom edge of the figure.
Precision Chart Development and Evaluation
Replicate determinations of reference samples were used to estimate precision. For each sample mixture having at least three determinations for water year 1998, the mean, standard deviation, and relative standard deviation (RSD) were calculated for each constituent. Taylor (1987, p. 20) defines RSD as the coefficient of variation multiplied by 100 (percent). The equation to represent this is:
| where | RSD | = relative standard deviation, |
| s | = standard deviation, and | |
| X | = mean of replicate values reported by the laboratory. |
The RSD provides an estimate of error relative to the mean of replicate values reported by the laboratory for each reference sample.
The RSD data are presented graphically as precision data charts in part B of figures 2 through 96 for the NWQL and figures 97 through 159 for the QWSU. These charts were prepared by plotting the RSD for inorganic, nutrient, and low-level constituents against the mean concentration of the reference samples reported by the individual laboratories. These charts allow a data reviewer to estimate precision at any concentration shown for a constituent. For example, figure 80B shows precision data for dissolved ammonia determinations from the NWQL. This plot shows a distribution of approximately 19 to 4 percent RSD for concentrations that range from 0.23 to 1.29 mg/L.
Precision is dependent upon the analyte of interest, the concentration range, the number of determinations, the method of determination, and the analyzing laboratory. A precision of 2-5 percent RSD is typical for chloride; whereas mercury's precision may vary from 10-40 percent RSD. Therefore, a data reviewer needs to be cognizant of the many variables contributing to a determinations precision and only compare for similar determinations.
To allow the precision charts to be used to estimate expected error of analytical results, outliers were rejected from the data set. Outliers are a rare occurrence in the data reported by the laboratories, accounting for less than 0.5 percent of all data. Outliers produce erroneous results in the use of parametric statistics such as RSD. Taylor (1987, p. 33-34) suggested NSD >=|4| as a criterion for rejection of data for a large sample set and NSD >=|6| for smaller data sets or when the standard deviation is not well established. In this report, an outlier was defined as a value greater than or equal to 6 standard deviations from the MPV. There were 48 outliers deleted from the entire data set of 11,056 analyses for the RSD procedure. Table 2 for the NWQL and table 3 for the QWSU present the total number of determinations for each constituent processed during the water year, the number of determinations that lie outside the ±2 standard deviation limits, and the number of determinations that lie outside the ±6 standard deviation limits.
The precision chart data for inorganic, nutrient, and low-level constituents have been separated into groups that are based on environmental-sample data quartiles in the same manner as explained previously in this report for the development of the control charts.
| where | P(x) | = probability of having x or more points greater than two standard deviations, |
| N | = number of successive points, and | |
| i | = number of points greater than two standard deviations. |
Analytical procedures exhibit imprecision if they have more determinations outside the control limits than the result predicted by the binomial equation. The binomial-probability-distribution procedure to measure precision allows tracking of annual variations in the precision of analytical measurements. The binomial test can be used to evaluate analytical results for short periods that appear to indicate imprecision, but the test loses power as fewer total analytical determinations are used in the evaluation.
There are two important factors to consider when analyzing analytical results for bias: the first is the number of observations in the subsample, and the second is the magnitude of the bias. If there are few observations in the subsample, the median difference has to be large to attain a p-value that indicates a biased condition. On the other hand, if there are many observations, a small median difference may result in a p-value that indicates bias.
The second factor used for the bias assessment is the bias magnitude. The magnitude of the bias is defined as the difference in concentration between the reported values from the laboratory and the MPV. The magnitude must be greater than one reporting unit for that MPV for the results to be considered biased. For example, 32 aluminum (DIS, ICP-MS) determinations of a sample having an MPV of 11.1 µg/L resulted in a median difference of 0.3 µg/L from the MPV. It is important to consider that at a concentration of 11.1 µg/L, a laboratory would typically report data only to the nearest 1 µg/L. The signed-rank test provided a p-value of 0.00247, which is considerably less than the 0.05 value. If the reporting unit was not considered, this result would have been considered biased negative, even though the laboratory was reporting the sample to the best of its reporting ability. Because the median difference of 0.3 µg/L is less than the reporting level of 1 µg/L, the magnitude of the bias is less than the implied accuracy of the analysis; therefore, analytical bias that is based strictly on the p-value has no practical meaning.
At the NWQL, positive analytical bias was indicated throughout the range of reference samples for chromium (DIS, ICP-AES), dissolved solids (DIS, GRAV), lithium (DIS, ICP-AES), and zinc (DIS, ICP-MS). Negative analytical bias throughout the reference sample range was indicated for silver (DIS, ICP-MS). This bias was caused by mix biases in the two samples submitted. Manganese (DIS, ICP-AES) showed a negative bias only on those mixes greater than 25 µg/L.
At the QWSU, positive bias was indicated throughout the range of reference samples for aluminum (WWR, ICP-AES/T). This bias was determined to be an artifact of the digestion process. Positive bias was indicated on the majority of sample mixes submitted for alkalinity (WWR, TITR) and dissolved solids (DIS, GRAV).
The statistical power of the Wilcoxon signed-ranks tests for analytical bias from QWSU is dependent on sample size. Tests on analytical data from the QWSU are less powerful than the same tests used at the NWQL due to the smaller sample sizes associated with the QWSU data.
At the NWQL, two mixes submitted for ammonia as nitrogen (DIS, COL, LL) and nitrate plus nitrite as nitrogen (DIS, COL, LL) showed a negative bias. There were no nutrient procedures at the QWSU that indicated a significant bias.
For each constituent, control charts were prepared on the basis of the difference between the analytical results and the most probable values of the reference samples. To allow the data for all reference mixes to be plotted on the same chart, the difference from the above calculations was divided by each sample's F-pseudosigma, which was determined from a linear-regression technique. Replicate sample determinations allowed the preparation of precision charts for each constituent. Data for inorganic, nutrient, and low-level constituent samples were then evaluated statistically for precision by using a binomial-probability-distribution test. The Wilcoxon signed-rank test was used in the bias assessment for each constituent by quantifying the median difference between the reported values and the most probable values.
An overall evaluation of the National Water Quality Laboratory inorganic and low-level constituent data for water year 1998 indicated imprecision for silver (dissolved, inductively coupled plasma-mass spectrometry). The evaluation also indicated bias throughout the range of reference samples for chromium (dissolved, inductively coupled plasma-atomic emission spectrometry), dissolved solids (dissolved, gravimetric), lithium (dissolved, inductively coupled plasma-atomic emission spectrometry), silver (dissolved, inductively coupled plasma-mass spectrometry), and zinc (dissolved, inductively coupled plasma-mass spectrometry).
Statistical evaluation of the National Water Quality Laboratory nutrient methods indicated a lack of precision for ammonia (dissolved, colorimetric) and orthophosphate as phosphorus (dissolved, colorimetric). Bias was indicated throughout the reference sample range for ammonia as nitrogen (dissolved, colorimetric, low level) and nitrate plus nitrite as nitrogen (dissolved, colorimetric, low level).
An overall evaluation of the Quality of Water Service Unit data for water year 1998 indicated no imprecision. Bias throughout the reference sample range was indicated for aluminum (whole-water recoverable, inductively coupled plasma-atomic emission spectrometry, trace).
Fishman, M.J., and Friedman, L.C., 1989, Methods for determination of inorganic substances in water and fluvial sediments: Techniques of Water-Resources Investigations of the U.S. Geological Survey, book 5, chap. A1, 545 p.
Friedman, L.C., Bradford, W.L., and Peart, D.B., 1983, Application of binomial distributions to quality assurance of quantitative chemical analyses: Journal of Environmental Science and Health, v. A18, no. 4, p. 561-570.
Friedman, L.C., and Erdmann, D.E., 1982, Quality assurance practices for the chemical and biological analyses of water and sediments: U.S. Geological Survey Techniques of Water-Resources Investigations, book 5, chap. A6, 181 p.
Helsel, D.R., and Hirsch, R.M., 1992, Statistical methods in water resources - Studies in environmental science, v. 49: Amsterdam, The Netherlands, Elsevier Science Publishers, 522 p.
Hoaglin, D.C., Mosteller, Frederick, and Tukey, J.W. 1983, Understanding robust and exploratory data analysis: New York, John Wiley, 447 p.
Janzer, V.J., 1985, The use of natural waters as U.S. Geological Survey reference samples, in Taylor, J.K., and Stanley, T.W., eds., Quality assurance for environmental measurements, ASTM STP 867: Philadelphia, American Society for Testing and Materials, p. 319-333.
Lucey, K.J., 1989, Quality-assurance data for routine water analysis in the National Water Quality Laboratory of the U.S. Geological Survey for water year 1988: U.S. Geological Survey Water- Resources Investigations Report 89-4166, 96 p.
Lucey, K.J., and Peart, D.B., 1988, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1985: U.S. Geological Survey Water-Resources Investigations Report 88-4109, 121 p.
---1989a, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1986: U.S. Geological Survey Water-Resources Investigations Report 89-4009, 145 p.
---1989b, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1987: U.S. Geological Survey Water-Resources Investigations Report 89-4049, 90 p.
Ludtke, A.S., Woodworth, M.T., and Marsh, P.S., 1999, Quality-assurance data for routine water analysis in U.S. Geological Survey laboratories, water year 1997: U.S. Geological Survey Water-Resources Investigations Report 99-4057, 186 p.
Maloney, T.J., Ludtke, A.S, and Krizman, T.L., 1992, Quality-assurance data for routine water analysis in the National Water Quality Laboratory of the U.S. Geological Survey for water year 1989: U.S. Geological Survey Water-Resources Investigations Report 92-4075, 99 p.
---1993, Quality-assurance data for the routine water analysis in the laboratories of the U.S. Geological Survey for water year 1990: U.S. Geological Survey Water-Resources Investigations Report 93-4082, 145 p.
---1994, Quality-assurance results for routine water analysis in U.S. Geological Survey laboratories, water year 1991: U.S. Geological Survey Water-Resources Investigations Report 94-4046, 144 p.
Peart, D.B., and Sutphin, H.B. 1987, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1984: U.S. Geological Survey Water-Resources Investigations Report 87-4077, 125 p.
Peart, D.B., and Thomas, Nancy, 1983a, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey 1981 annual report: U.S. Geological Survey Water-Resources Investigations Report 83-4090, 112 p.
---1983b, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1982: U.S. Geological Survey Water-Resources Investigations Report 83-4264, 112 p.
---1984, Quality-assurance data for routine water analysis in the laboratories of the U.S. Geological Survey for water year 1983: U.S. Geological Survey Water-Resources Investigations Report 84-4234, 112 p.
Schroder, L.J., Fishman, M.J., Friedman, L.C., and Darlington, G.W., 1980, The use of standard reference water samples by the U.S. Geological Survey: U.S. Geological Survey Open-File Report 80-738, 11 p.
Skougstad, M.W., and Fishman, M.J., 1975, Standard reference water samples: American Water Works Association Water Quality Technology Conference, Dallas, 1974, Proceedings, p. XIX-1-XIX-6.
Taylor, J.K., 1987, Quality assurance of chemical measurements: Chelsea, Mich., Lewis Publishers, 328 p.
| For addition information write to: | Copies of this report can be purchased from: |
|---|---|
| Chief, Branch of Quality Systems
U.S. Geological Survey Water Resources Division Box 25046, Mail Stop 401 Denver Federal Center Denver, CO 80225-0046 |
U.S. Geological Survey
Branch of Information Services Box 25286 Denver Federal Center Denver, CO 80225-0286 |